如果你在使用示波器時，因采集到的無效波形過多，導致有效波形失真，又或者你在捕獲異常時，想獲得每次異常現象，那么這里提到的分段存儲功能，可能就是你想要的答案。

波形失真案例分析

我們采集一段波形CAN總線信號，用ZDS5054 Pro示波器對該信號進行采集并顯示。第一次實驗我們將示波器存儲深度設置為1.4Mpts，采樣時間設置為280us，采集完成一幀波形并按下暫停后，將波形調整至合適位置，波形和解碼結果如圖1所示，此時屏幕時基為10us/div。第二次實驗我們將示波器存儲深度同樣設置為1.4Mpts，但采樣時間設置為700ms，采集完成并按下暫停后將波形調整為第一次實驗設置的參數即10us/div，獲得的一幀CAN總線波形和解碼結果如圖2所示。

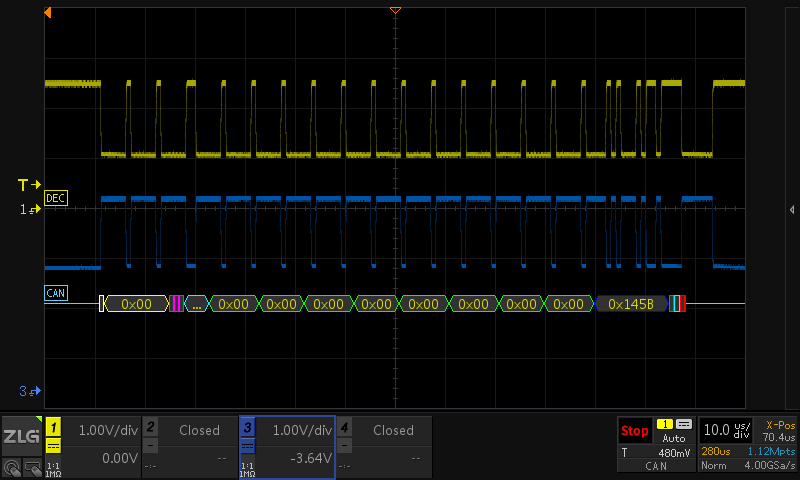
圖1 存儲深度1.4Mpts、采樣時間280us波形結果的部分

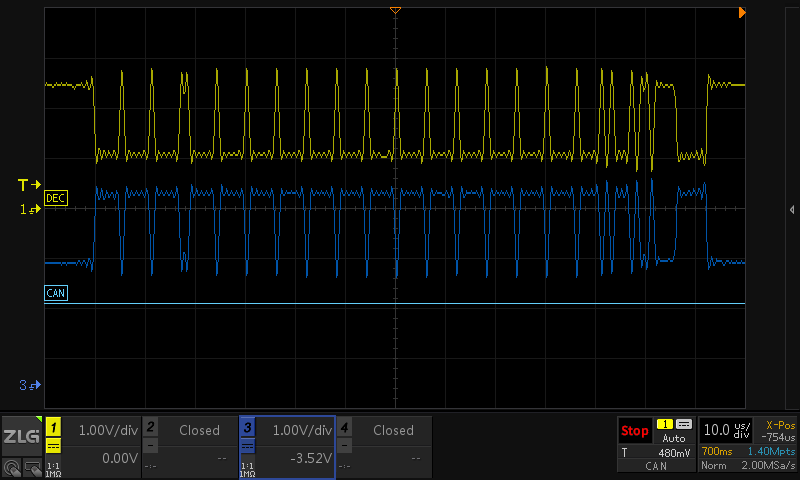
圖2 存儲深度1.4Mpts、采樣時間700ms波形結果的部分

很明顯，在不同的時間采樣下，圖2的波形存在很大程度的失真，導致系統解碼解析不出來。這里導致失真的主要原因和存儲深度及采樣率有一定的關系。對于采樣率 Fs、存儲深度 N，及捕獲時間 T（本實驗中設置的采樣時間T）三者必然滿足如下關系式：N = Fs *T。

當我們存儲深度固定時，增加捕獲時間T，必然導致采樣率的降低，根據奈奎斯特采樣定理，若 Fs 低于被測信號頻率的 2 倍，將存在混疊現象，此時顯示的波形具有迷惑性，是不可靠的。圖1采樣率為4Gsa/s，而圖2因為T的增大而導致采樣率僅剩2MSa/s，因此出現上述的圖2波形失真的問題。實際上，一般采樣率要在信號頻率的 4~5 倍左右波形才是有保證的。

對比圖1和圖2，可能還會有小伙伴疑惑為什么設置同樣的存儲深度1.4Mpts，圖1僅達到 1.12Mpts，而圖2卻能達到1.40Mpts，這僅僅是因為上述的關系式N = Fs *T導致的，T為固定的值幾個數值變化，必然需要相應固定的存儲深度和4GSa/s相乘，為策略性問題。

采用分段存儲方式解決失真問題

我們將上述的圖2水平時基檔位變大，即1ms/div，如圖3所示，可以看到我們采集到的CAN總線信號有很大一部分時間采集的其實都是無用信息，這是因為應用程序對CAN總線的控制通信是有時間間隔的。

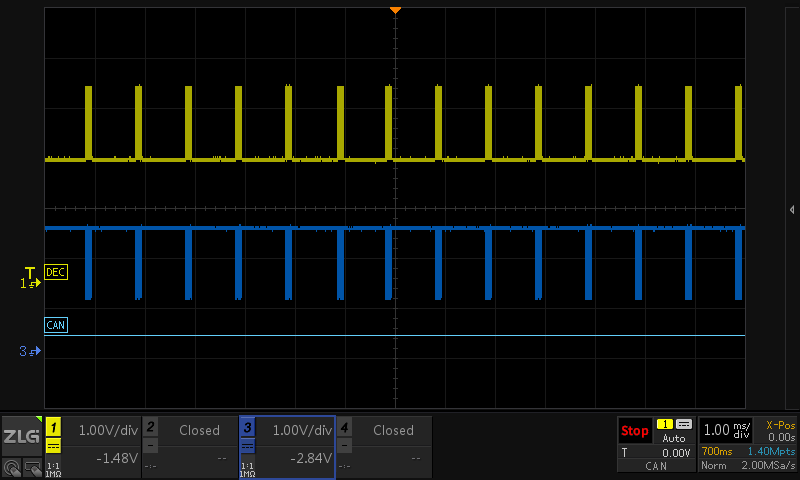
圖3 存在通信時間間隔的CAN信號

如果我們此時只想獲得通信的數據內容，而無需幀與幀之間的等待時間，那么此間隔對采集數據來說并無意義，這時候我們是不是就可以考慮讓示波器只記錄有用信息的那一段，無用信息的那段就不記錄，這樣不就可以節省大量的存儲深度，從而緩解甚至解決之前出現的那種失真問題了嗎？所以，此處便是我們講解的重點功能——分段存儲。如圖4通過設定CAN的起始位為觸發條件，從而利用分段存儲功能獲得511幀CAN信號波形，并且每一幀波形都不存在失真。

圖4 分段存儲CAN信號

分段存儲的原理

由上述例子，相信我們對分段存儲有了一定的概念理解。所謂分段存儲，既通過設置觸發的方式，對每次觸發采樣得到的數據存放到各段的存儲空間中，從而可以更高效地利用示波器的存儲深度且保證波形細節，并且也能夠在足夠的采樣率下捕獲多個波形事件，以便進行有效的分析。

存儲原理如下圖 5所示，總的存儲深度分為 n 段，第 1 段用于顯示，第 2 段開始存儲，也就是當發生第一次觸發時采集的數據存儲到第2段存儲空間中（此處不同示波器的策略可能存在差異，但觸發后再存儲的本質沒變化），當第2段存儲空間存儲滿之后， 結束第一次觸發，等待第二次觸發的到來，觸發后把數據存儲到第 3 段存儲空間中，以此類推。

圖5 分段采集原理