ua、ub 、uc 為三相定子繞組電壓；

Ra 、Rb 、Rc 為三相定子繞組電阻，大小均為R ；

ia 、ib 、ic 為三相定子繞組電流；

ψa ，ψb，ψc 為三相定子繞組的磁鏈；

L為三相定子繞組的自感，包括漏電感分量和主電感分量；

ψf 為轉子永磁磁鏈；

θe 為轉子軸線與A 相繞組軸線夾角的電氣角度。

在永磁同步電機數學模型研究中，經常用到如圖5~7所示三個坐標系，它們是靜止的abc 坐標系、靜止的αβ 坐標系和旋轉的dq 坐標系。坐標系之間可以進行相互變換，如abc坐標系到αβ 坐標系的坐標系變換稱之為Clark 變換，αβ 坐標系到dq 坐標系的變化則是Park 變換。

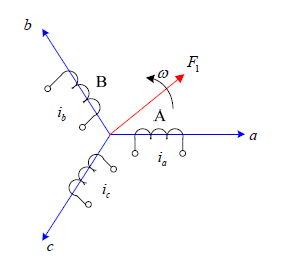
abc坐標系

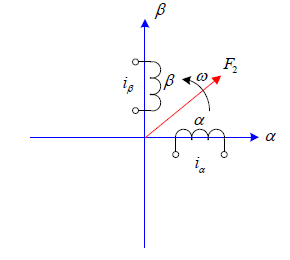
αβ坐標系

dq坐標系

三相交流繞組電路，假設繞組A、B、C通以時間上相差120、角速率為ω 的三相對稱正弦電流。那么三相電流將產生合成的磁動勢 F1 ，它在空間成正弦分布，與交流電同頻順著A? B ?C相序來旋轉；兩相繞組α 和β ，它們在空間上相差90。當通以時間上相差90、角速率為ω 的兩相平衡正弦電流時，也能產生空間上為圓形、角速度為ω 、磁動勢為 F2 的旋轉磁場；在旋轉坐標系dq 中，如果在匝數相等且互相垂直的繞組d 和繞組q 中分別通以直流電流。兩相直流電流能夠產生合成的磁動勢F3 。由于兩個繞組以同步角速度ω 一起旋轉，則磁動勢F3 也會隨之成為旋轉磁動勢。經過坐標變換之后，即可獲得系統的微分方程如下所示：

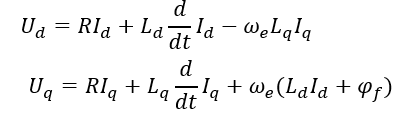
（２）電機矢量控制策略

考慮到一般的PMSM 伺服系統的功率不大，但對于過載能力以及轉矩響應特性有比較高的要求。并且id = 0 控制方法比較簡單，電機的輸出轉矩與定子電流的幅值成線性關系，且無去磁效應。因此，采用如圖所示的PMSM矢量控制策略。

id = 0 的控制方案要求，在電機運行過程中，系統通過不斷檢測電機轉子角位置，進而改變定子合成電流矢量is 的大小和方向，使is 的直軸分量滿足id = 0，交軸分量iq = is。（這樣一來，電機定子電流所形成的電樞磁場將一直與電機轉子軸垂直，實際交軸電流也與設定的定子合成電流值相等，）即所有的電流都用來使電機輸出電磁轉矩，逆變器也無需為電機提供無功勵磁電流。此種方案下電磁轉矩輸出平穩、響應迅速，因此電機能夠很好的啟動與制動，調速性能較好，調速范圍也寬。

矢量控制策略

伺服系統屬于串級控制系統，由速度環和電流環組成。速度環的作用是使電機的轉速跟蹤設定轉速，能夠控制電機加減速，增強系統抗負載擾動的能力，抑制速率波動。電流環的作用是根據速度環給定的力矩電流值和檢測的電機相電流值，使控制器產生實時的空間矢量PWM 波形（的控制電壓信號），進而通過逆變器來改變電機相電流值。

（3）仿真驗證

在PSIM軟件中結合以上分析搭建如圖所示可生成代碼的數字仿真電路，其仿真與實驗結果如圖所示。

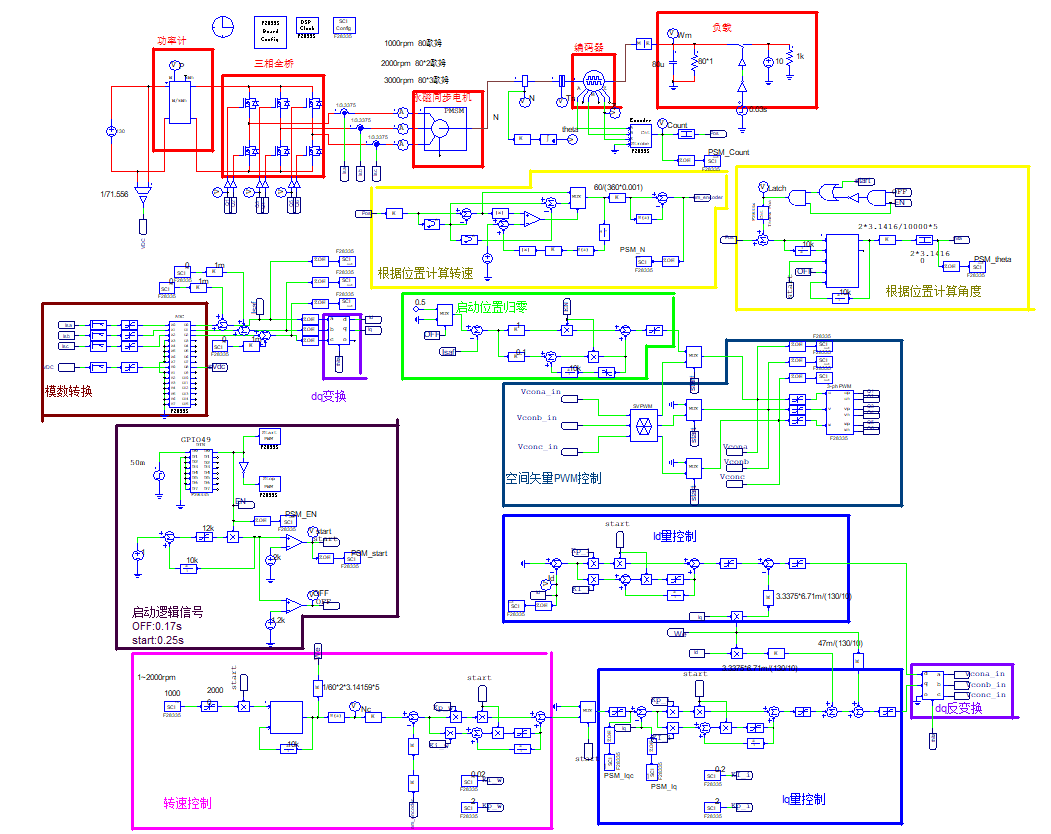
PMSM矢量控制電路

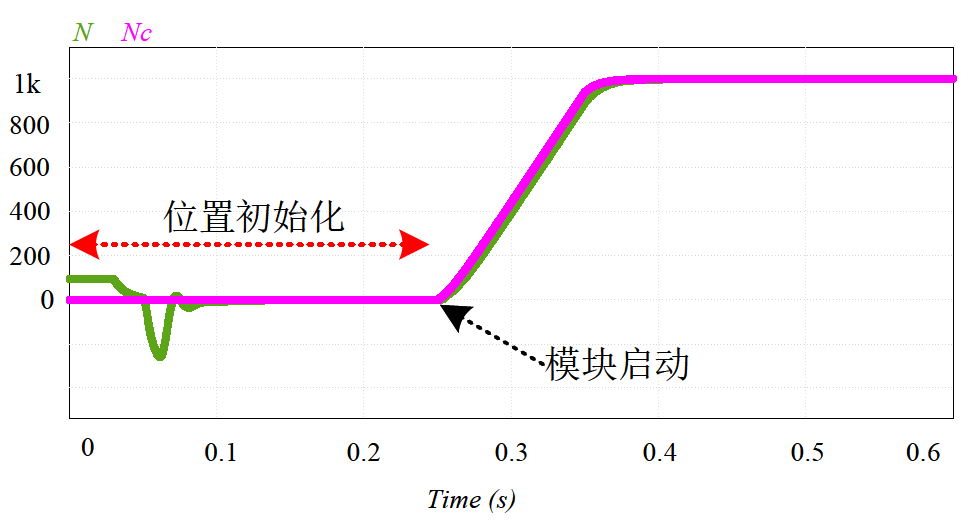
電機轉速與給定

結　論：