在電子測量領域,數字示波器與模擬示波器有著顯著區別。數字示波器具備豐富的測量參數,諸如上升時間、下降時間、峰峰值以及幅值等。通常而言,這些參數的定義在示波器操作手冊中均有詳細說明。然而,若深入探究每個參數底層算法的根源,會發現其中蘊含的原理并不簡單。透徹理解示波器的基本算法,對于我們理解使用示波器過程中遭遇的復雜問題大有裨益。比如,為何光標測量結果與參數測量結果存在較大差異?為何示波器在測量不規則信號的上升時間時,跳變范圍較大?接下來,由鼎陽科技為大家詳細解讀數字示波器測量參數中的關鍵算法 —— 垂直測量的第一算法。
那么,究竟什么是數字示波器的第一算法呢?在此,我們將示波器中用于確定高電平和低電平的算法,定義為數字示波器垂直量測量的第一算法。
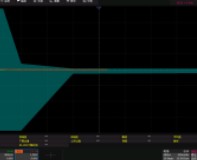
數字示波器垂直量測量的第一算法核心在于確定高電平和低電平。峰值的概念相對直觀,即所有采樣樣本中的最大樣本值減去最小樣本值,這在數字示波器算法的實現上并不復雜。而幅值則是指被測信號的 “高電平” 減去 “低電平”。但問題在于,高電平和低電平具體處于何處呢?這就需要借助特定算法來明確。該算法的確定意義重大,它不僅直接決定了 “幅值” 這一參數的值,還會對絕大多數與水平軸相關的參數,如上升時間、下降時間、寬度以及周期等產生影響,因為這些水平軸參數的計算依賴于垂直軸參數。
在數字示波器的算法體系中,一般默認依據屏幕最左側到最右側的全部波形數據來確定 “高電平” 和 “低電平”。因此,數字示波器每進行一次捕獲操作,僅能獲取一組 “高電平” 和 “低電平” 的參數值。
值得注意的是,測量單個脈沖方波與測量多個脈沖方波時,所得到的 “高電平” 和 “低電平” 結果可能會有所不同。這是由于統計的樣本數量不同,進而導致生成的 “軌跡直方圖” 存在差異。倘若信號存在些許過沖或下沖現象,就可能干擾直方圖分布中最大概率狀態的確定,如此一來,眾多參數的測量結果都會受到波及。在實際測量過程中,我們務必對此予以高度關注。
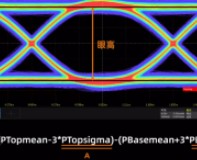
當測量 “頂部” 數據樣本稀缺的波形時,經統計形成的 “軌跡直方圖” 可能無法呈現出明顯的高概率密度位置。例如,在測量正弦波時,由于其 “頂部” 數據量較少,不存在概率密度顯著偏高的位置。此時,部分數字示波器算法會將波形的 “最大值” 認定為 “高電平”,“最小值” 認定為 “低電平”。
以上便是對數字示波器垂直量測量第一算法的詳細介紹。在測量正弦波時,若采樣率充足,數字示波器捕獲到的波形數量越多,所測量得到的高電平和低電平就越穩定、準確。相應地,受其影響的水平軸參數,如上升時間、下降時間、周期以及頻率等,也會更加精準。對于正弦波的測量,還可借助正弦插值或等效采樣模式來增加待分析的樣本數量,如此一來,測量結果可能會更為精確 。
那么,究竟什么是數字示波器的第一算法呢?在此,我們將示波器中用于確定高電平和低電平的算法,定義為數字示波器垂直量測量的第一算法。
數字示波器垂直量測量的第一算法核心在于確定高電平和低電平。峰值的概念相對直觀,即所有采樣樣本中的最大樣本值減去最小樣本值,這在數字示波器算法的實現上并不復雜。而幅值則是指被測信號的 “高電平” 減去 “低電平”。但問題在于,高電平和低電平具體處于何處呢?這就需要借助特定算法來明確。該算法的確定意義重大,它不僅直接決定了 “幅值” 這一參數的值,還會對絕大多數與水平軸相關的參數,如上升時間、下降時間、寬度以及周期等產生影響,因為這些水平軸參數的計算依賴于垂直軸參數。
在數字示波器的算法體系中,一般默認依據屏幕最左側到最右側的全部波形數據來確定 “高電平” 和 “低電平”。因此,數字示波器每進行一次捕獲操作,僅能獲取一組 “高電平” 和 “低電平” 的參數值。
值得注意的是,測量單個脈沖方波與測量多個脈沖方波時,所得到的 “高電平” 和 “低電平” 結果可能會有所不同。這是由于統計的樣本數量不同,進而導致生成的 “軌跡直方圖” 存在差異。倘若信號存在些許過沖或下沖現象,就可能干擾直方圖分布中最大概率狀態的確定,如此一來,眾多參數的測量結果都會受到波及。在實際測量過程中,我們務必對此予以高度關注。
當測量 “頂部” 數據樣本稀缺的波形時,經統計形成的 “軌跡直方圖” 可能無法呈現出明顯的高概率密度位置。例如,在測量正弦波時,由于其 “頂部” 數據量較少,不存在概率密度顯著偏高的位置。此時,部分數字示波器算法會將波形的 “最大值” 認定為 “高電平”,“最小值” 認定為 “低電平”。
以上便是對數字示波器垂直量測量第一算法的詳細介紹。在測量正弦波時,若采樣率充足,數字示波器捕獲到的波形數量越多,所測量得到的高電平和低電平就越穩定、準確。相應地,受其影響的水平軸參數,如上升時間、下降時間、周期以及頻率等,也會更加精準。對于正弦波的測量,還可借助正弦插值或等效采樣模式來增加待分析的樣本數量,如此一來,測量結果可能會更為精確 。