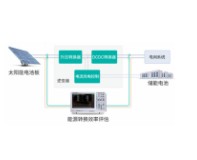
作者：陳博
橫河的功率分析儀都有一個(gè)平均功能，這個(gè)功能包含兩種平均化方法，分別是指數(shù)平均和移動(dòng)平均(也叫線性平均)。平均功能針對電源或負(fù)載的變動(dòng)較大或輸入信號的頻率較低時(shí)數(shù)值顯示不穩(wěn)定、讀取困難的情況有效。雖然都有詳細(xì)的計(jì)算公式說明，但很多工程師在實(shí)際使用中往往無法區(qū)分這兩種平均化方式，以及使用使用場景上的區(qū)別，本文通過計(jì)算圖表做簡單的說明。
首先，簡單介紹這種平均化的公式：
指數(shù)平均
可以通過設(shè)定的衰減常數(shù)將數(shù)據(jù)指數(shù)平均，并根據(jù)以下公式求得平均值。
Dn: 經(jīng)過第n次指數(shù)平均后顯示的數(shù)值(第1次顯示的數(shù)值D1等于M1)。
Dn–1: 經(jīng)過第n-1次指數(shù)平均后顯示的數(shù)值。
Mn: 第n次的測量數(shù)據(jù)。
K: 衰減常數(shù)(從2、4、8、16、32、64中選擇)。
移動(dòng)平均
可以通過設(shè)定的平均個(gè)數(shù)將數(shù)據(jù)線性平均，并根據(jù)以下公式求得平均值。
Dn: 將第n–(m–1)次到第n次的m個(gè)數(shù)值數(shù)據(jù)線性平均后顯示的數(shù)值
Mn–(m–1): 第n–(m–1)次的測量數(shù)據(jù)。
……
Mn–2: 第n–2次的測量數(shù)據(jù)
Mn–1: 第n–1次的測量數(shù)據(jù)
Mn: 第n次的測量數(shù)據(jù)
m: 平均個(gè)數(shù)(從8、16、32、64、128、256中選擇)。
如果只是粗略地看這兩個(gè)公式，雖然運(yùn)算上有很大的區(qū)別，但無法讓工程師直觀地理解這種平均化運(yùn)算對實(shí)測測試結(jié)果有多大的影響，具體平滑處理到什么程度，衰減常數(shù)應(yīng)該如何選擇。下文選取了一段WT5000的DS功能記錄的原始波形，利用EXCEL將兩種平均方式按不同的衰減常數(shù)做了簡單的運(yùn)算，并將運(yùn)算結(jié)果與原始波形一起做對比。
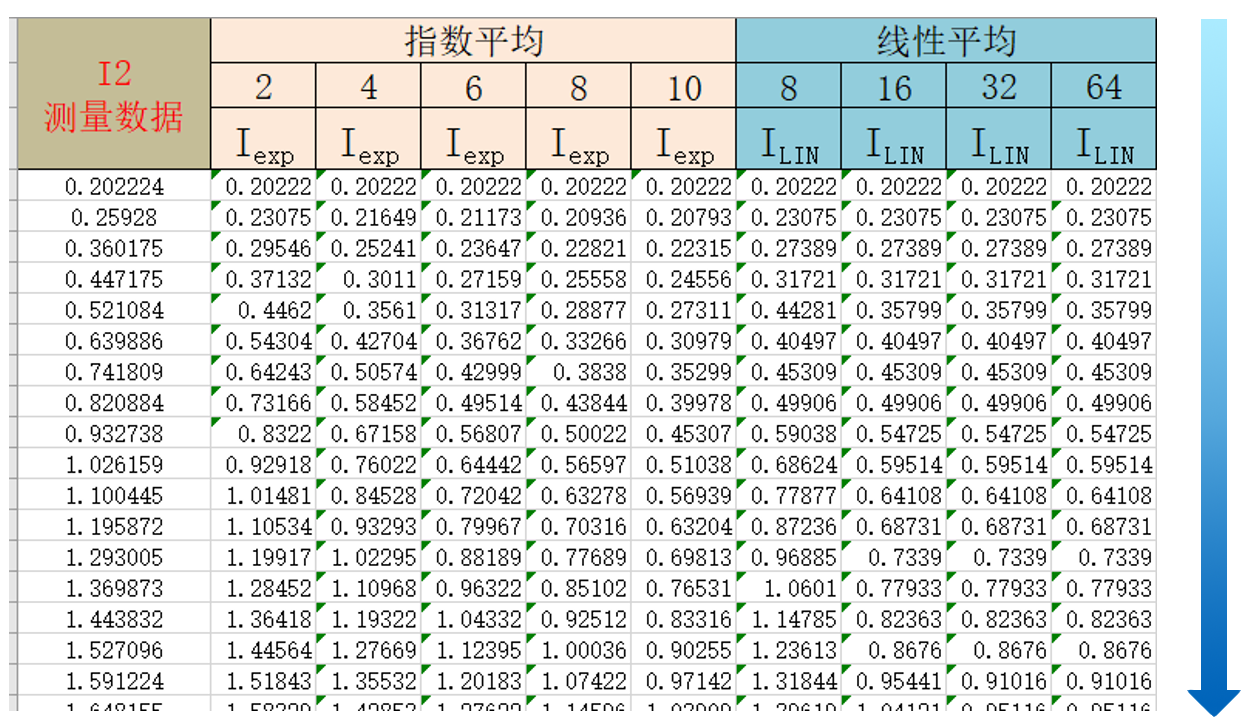
因?yàn)樯婕斑\(yùn)算量比較多，這里就選取了指數(shù)平均衰減常數(shù)2、4、6、8、10，移動(dòng)平均衰減常數(shù)8、16、32、64為例。上圖中截選了一小部分的運(yùn)算結(jié)果，當(dāng)然我們只是從這個(gè)運(yùn)算結(jié)果無法對這兩種平均化方式有任何直觀的認(rèn)識，那么把所有的運(yùn)算數(shù)據(jù)導(dǎo)入二維圖表，就能比較清晰的看出區(qū)別了。
指數(shù)平均＆移動(dòng)平均運(yùn)算結(jié)果
首先，原始波形在尖峰部分以及下降部分有鋸齒形狀的波動(dòng)，無論是指數(shù)平均或移動(dòng)平均采用8以上的衰減常數(shù)，都能很好地平滑波形曲線。但移動(dòng)平均在最低8的衰減參數(shù)影響下會(huì)出現(xiàn)明顯的相移，隨著衰減次數(shù)的增加，相移與尖峰部分的平滑會(huì)急劇上升。與移動(dòng)平均相比，指數(shù)平均雖然隨著衰減常數(shù)遞增，也會(huì)出現(xiàn)相移以及波峰的平滑，但總體來說，波形的形狀并不會(huì)有明顯的改變。
本文為了做對比，采用了較大的指數(shù)平均衰減常數(shù)（移動(dòng)平均衰減常數(shù)只能選擇8、16…..）,而實(shí)際測試中，我們可以設(shè)置較小的指數(shù)平均衰減常數(shù)如2、4、6等，這樣的話對于波峰的平滑以及相移可以做到較好的權(quán)衡處理。實(shí)際應(yīng)用中，因?yàn)樵紨?shù)據(jù)是積分處理后RMS或者有功等值，波動(dòng)很少會(huì)如案例中這么劇烈，如果只是針對突發(fā)性的數(shù)據(jù)波動(dòng)，可以采用較低次數(shù)的指數(shù)平均，平滑數(shù)值曲線，對于實(shí)際讀數(shù)也不會(huì)有明顯的延遲。
但如果對于較為劇烈波動(dòng)的數(shù)值曲線平滑處理，可以考慮采用高次數(shù)的指數(shù)平均或者低次數(shù)的移動(dòng)平均。對于移動(dòng)平均的衰減參數(shù)選擇需要謹(jǐn)慎處理，較大的衰減參數(shù)會(huì)完全改變測量數(shù)值的波動(dòng)曲線，導(dǎo)致錯(cuò)誤的測量結(jié)果。
更多技術(shù)詳情，歡迎聯(lián)系橫河工程師。
